Önceki paylaşımlarda 1.dereceden 2 bilinmeyenli ve 3 bilinmeyenli denklemlerin çözümüne yönelik matlab yapay sinir ağı örneği yer almıştı. Bu çalışmada ise 2.dereceden 2 bilinmeyenli bir denklemin 3 farklı yapay sinir ağı yöntemi ile Matlab'da çözümü gösterilmiştir.
Bu çalışmada y=2*(x1)2+5*Sin(x2)+x1*x2 denkleminin Yapay Sinir Ağlarının Normal Geri Yayılım Yöntemi, Newton Yöntemi, Levenberg-Marquardt Yöntemi İle Matlab'da çözümünü yer almaktadır.
1-y=2*(x1)2+5*Sin(x2)+x1*x2 denkleminin Yapay Sinir Ağları Geri Yayılım metodu ile çözümünde kullanılacak Matlab kodu aşağıdaki gibidir:
close all
clear all
clc
t=0:.1:20;
x1=100*sin(2*pi*t/10);
x2=100*sin(2*pi*t/15);
x0=1;
d1=2*x1.^2+5*sin(x2)+x1.*x2;
x=[x1;x2];
d=d1./max(d1);
w1=rand(6,2); w10=rand(6,1);
w2=rand(6,1); w20=rand;
load erkw
alfa=0.034;
E=10; s=0;
while (s<1000)
s=s+1;
for i=1:201
v=w1*(x(:,i)./100)+w10;
f=(1-exp(-v))./(1+exp(-v));
y(i)=w2'*f+w20;
e(i)=d(i)-y(i);
delta_w2=e(i)*f;
delta_w20=e(i);
delta_w1=(e(i)*(f.*(1-f)).*w2)*(x(:,i)./100)';
delta_w10=e(i)*(f.*(1-f)).*w2;
w1=w1+alfa*delta_w1;
w2=w2+alfa*delta_w2;
w10=w10+alfa*delta_w10;
w20=w20+alfa*delta_w20;
end
E=.5*sumsqr(e);
JJ(s)=E;
if (mod(s,100)==0)
s,E
end
end
plot(y*max(d1),'*')
hold on
plot(d1,'r')
save erkw.mat w1 w10 w2 w20
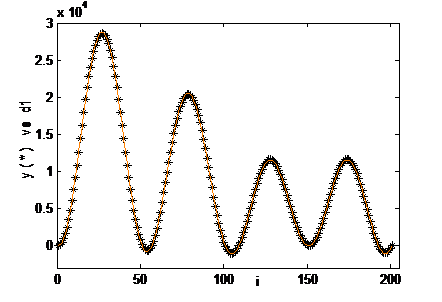
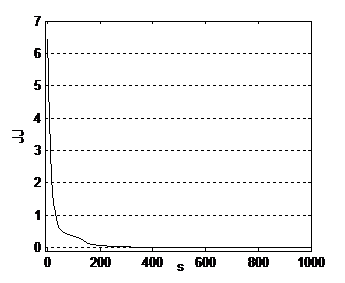
2- y=2*(x1)2+5*Sin(x2)+x1*x2 denkleminin Newton metodu ile çözümünde kullanılacak Matlab kodu aşağıdaki gibidir:
clc
clf
clear
w=randn(5,2);
w2=randn(1,5);
q=randn;
birim=eye(5,5);
birim1=eye(2,2);
bir=eye(26,26);
lamda=10000;
dw=zeros(5,2);
dw2=zeros(1,5);
dq=zeros;
alfa=.55;
for k=1:20
x1(k)=sin(k*pi/20);
x2(k)=cos(k*pi/20);
y(k)=2*x1(k)^2+5*sin(x2(k))+x1(k)*x2(k);
end
x=[x1; x2];
figure(1)
for i=1:500
o=w*x;
v=(1-exp(-o))./(1+exp(-o));
ym=w2*v+q*ones(1,k);
e=y-ym;
j=-v';
h=j'*j;
g=j'*e';
d=(1-v.^2).*(w2'*(-1*ones(1,size(e,2))));
d1=[d(1,:)' d(1,:)'];
d2=[d(2,:)' d(2,:)'];
d3=[d(3,:)' d(3,:)'];
d4=[d(4,:)' d(4,:)'];
d5=[d(5,:)' d(5,:)'];
j11=d1.*x';
j12=d2.*x';
j13=d3.*x';
j14=d4.*x';
j15=d5.*x';
j11h=j11'*j11;
j12h=j12'*j12;
j13h=j13'*j13;
j14h=j14'*j14;
j15h=j15'*j15;
h11h(1,:)=j11h(1,:)*j11h(1,1);
h11h(2,:)=j11h(2,:)*j11h(2,2);
h12h(1,:)=j12h(1,:)*j12h(1,1);
h12h(2,:)=j12h(2,:)*j12h(2,2);
h13h(1,:)=j13h(1,:)*j13h(1,1);
h13h(2,:)=j13h(2,:)*j13h(2,2);
h14h(1,:)=j14h(1,:)*j14h(1,1);
h14h(2,:)=j14h(2,:)*j14h(2,2);
h15h(1,:)=j15h(1,:)*j15h(1,1);
h15h(2,:)=j15h(2,:)*j15h(2,2);
hh(1,:)=h(1,:)*h(1,1);
hh(2,:)=h(2,:)*h(2,2);
hh(3,:)=h(3,:)*h(3,3);
hh(4,:)=h(4,:)*h(4,4);
hh(5,:)=h(5,:)*h(5,5);
jq=(-1*ones(1,size(e,2)))';
jqh=jq'*jq;
gq=jq'*e';
g1=j11'*e';
g2=j12'*e';
g3=j13'*e';
g4=j14'*e';
g5=j15'*e';
w(1,:)=w(1,:)-alfa*((1/2)*(j11h+lamda*inv(h11h))\g1)';
w(2,:)=w(2,:)-alfa*((1/2)*(j12h+lamda*inv(h12h))\g2)';
w(3,:)=w(3,:)-alfa*((1/2)*(j13h+lamda*inv(h13h))\g3)';
w(3,:)=w(4,:)-alfa*((1/2)*(j14h+lamda*inv(h14h))\g4)';
w(5,:)=w(5,:)-alfa*((1/2)*(j15h+lamda*inv(h15h))\g5)';
w2=w2-alfa*((1/2)*(h+lamda*inv(hh))\g)';
q=q-alfa*(1/2)*(jqh+lamda*inv(jqh*jqh))\gq;
%alfa=alfa*(1.01);
E(i)=sumsqr(e)/k;
ploterr(E(1:i))
end
plot(y)
hold on
plot(ym,'r*')
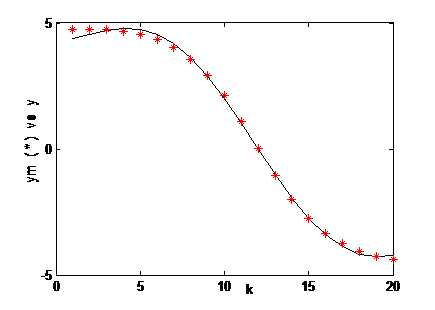
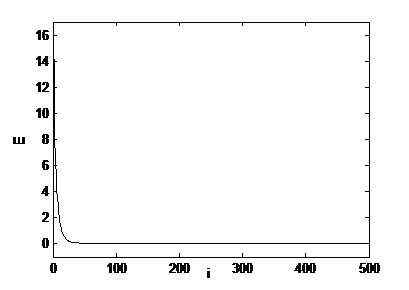
Şekil 2. Newton Metodu ile Yapılan Çözümün Erkan Çıktıları
2- y=2*(x1)2+5*Sin(x2)+x1*x2 denkleminin YSA'nın Levenberg –Marquardt Yöntemi ile çözümünde kullanılacak Matlab kodu aşağıdaki gibidir:
clc
clf
clear
w=randn(5,2);
w2=randn(1,5);
q=randn;
birim=eye(5,5);
birim1=eye(2,2);
bir=eye(26,26);
lamda=10000;
dw=zeros(5,2);
dw2=zeros(1,5);
dq=zeros;
alfa=.55;
for k=1:20
x1(k)=sin(k*pi/20);
x2(k)=cos(k*pi/20);
y(k)=2*x1(k)^2+5*sin(x2(k))+x1(k)*x2(k);
end
x=[x1; x2];
figure(1)
for i=1:500
o=w*x;
v=(1-exp(-o))./(1+exp(-o));
ym=w2*v+q*ones(1,k);
e=y-ym;
j=-v';
h=j'*j;
g=j'*e';
d=(1-v.^2).*(w2'*(-1*ones(1,size(e,2))));
d1=[d(1,:)' d(1,:)'];
d2=[d(2,:)' d(2,:)'];
d3=[d(3,:)' d(3,:)'];
d4=[d(4,:)' d(4,:)'];
d5=[d(5,:)' d(5,:)'];
j11=d1.*x';
j12=d2.*x';
j13=d3.*x';
j14=d4.*x';
j15=d5.*x';
j11h=j11'*j11;
j12h=j12'*j12;
j13h=j13'*j13;
j14h=j14'*j14;
j15h=j15'*j15;
h11h(1,:)=j11h(1,:)*j11h(1,1);
h11h(2,:)=j11h(2,:)*j11h(2,2);
h12h(1,:)=j12h(1,:)*j12h(1,1);
h12h(2,:)=j12h(2,:)*j12h(2,2);
h13h(1,:)=j13h(1,:)*j13h(1,1);
h13h(2,:)=j13h(2,:)*j13h(2,2);
h14h(1,:)=j14h(1,:)*j14h(1,1);
h14h(2,:)=j14h(2,:)*j14h(2,2);
h15h(1,:)=j15h(1,:)*j15h(1,1);
h15h(2,:)=j15h(2,:)*j15h(2,2);
hh(1,:)=h(1,:)*h(1,1);
hh(2,:)=h(2,:)*h(2,2);
hh(3,:)=h(3,:)*h(3,3);
hh(4,:)=h(4,:)*h(4,4);
hh(5,:)=h(5,:)*h(5,5);
jq=(-1*ones(1,size(e,2)))';
jqh=jq'*jq;
gq=jq'*e';
g1=j11'*e';
g2=j12'*e';
g3=j13'*e';
g4=j14'*e';
g5=j15'*e';
w(1,:)=w(1,:)-alfa*((1/2)*(j11h+lamda*inv(h11h-0.01*birim1))\g1)';
w(2,:)=w(2,:)-alfa*((1/2)*(j12h+lamda*inv(h12h-0.01*birim1))\g2)';
w(3,:)=w(3,:)-alfa*((1/2)*(j13h+lamda*inv(h13h-0.01*birim1))\g3)';
w(3,:)=w(4,:)-alfa*((1/2)*(j14h+lamda*inv(h14h-0.01*birim1))\g4)';
w(5,:)=w(5,:)-alfa*((1/2)*(j15h+lamda*inv(h15h-0.01*birim1))\g5)';
w2=w2-alfa*((1/2)*(h+lamda*inv(hh-0.01*birim))\g)';
q=q-alfa*(1/2)*(jqh+lamda*inv(jqh*jqh-0.01))\gq;
%alfa=alfa*(1.01);
E(i)=sumsqr(e)/k;
ploterr(E(1:i))
end
plot(y)
hold on
plot(ym,'r*')
%xlabel('Agirlik (w)')
%ylabel('Polarma Agirligi (b)')
%title('Hata Egrisi')
NOT : Sitede, yapay sinir ağı, yapay sinir ağları nelerdir, derin öğrenme nedir, deep learning nedir, bulanık mantık nedir, fuzzy logic nedir, yapay sinir ağları uygulamaları, makine öğrenmesi, yapay sinir ağı algoritmaları, makine öğrenmesi ve derin öğrenme, regresyon, machine learning nedir, matlab, matlab örnekleri, matlab machine learning gibi soruların cevaplarına yönelik içerikler yer almaktadır. 'Yapay sinir ağı’, ‘yapay sinir ağları nedir’, ‘derin öğrenme nedir’, ‘deep learning nedir’, ’bulanık mantık nedir’, ‘fuzzy logic nedir’, ‘yapay sinir ağları uygulamaları’, ‘makine öğrenmesi’, ‘yapay sinir ağı algoritmaları’, ‘makine öğrenmesi ve derin öğrenme’, regresyon, ‘machine learning nedir’, matlab, ‘matlab örnekleri’, ‘matlab machine learning’, 'artificial neural network','ysa ile denklem çözümü', 'ysa 2 bilinmeyenli denklem', 'yapay sinir ağları 3 bilinmeyenli denklem', 'and kapısı ve ysa', 'and gate ysa', 've kapısı matlab', 'and gate ve kapısı', 'or kapısı ve ysa', 'or gate ysa', 'veya kapısı matlab', 'or gate veya kapısı', 'xor kapısı ve ysa', 'xor gate ysa', 'özel veya kapısı matlab', 'xor gate özel veya kapısı' ,'levenberg-marquardt yöntemi','newton yöntemi', 'geri yayılım algoritması'
--->>> YSA ile XOR Kapısı Problem Çözümü için TIKLAYINIZ <<<---
--->>> Matlab'da Analitik Yöntem & Euler Metodu karşılaştırması için TIKLAYINIZ <<<---
--->>> YSA ile 2 Bilinmeyenli Denklem Çözümü için TIKLAYINIZ <<<---
--->>> YSA ile 1.Dereceden 3 Bilinmeyenli Denklem Çözümü için TIKLAYINIZ <<<---
